Data Science in Quant Finance Index Forecasting

概要

自2018年末以来，全球金融市场从稳步上升变得起伏不定。投资者对市场走向和未来展望的不确定，导致大盘和指数波动加剧。中美贸易战带来的关税压力使市场情绪低迷；2020年初，新冠肺炎疫情全球蔓延，医疗资源紧张，防控措施减缓了商品和人员流动，多地商店停业甚至倒闭，严重影响了经济生活，全球股市出现熔断和跌停。政府和金融监管机构推行各类政策应对疫情影响，稳定经济和金融市场。

对许多金融从业者而言，市场动荡带来新的投资机遇，但2008年金融危机的教训提醒我，机遇背后伴随着巨大风险。著名的《巴塞尔协定III》在应对全球金融危机和强化金融监管的背景下诞生，被广泛用于各大金融机构。识别风险、保障资产安全并保持流动性是风险管理的重要部分。在股票市场风险管理中，金融从业者需要先查看价格变化是否在预期范围内，并判断这些变化是由系统风险还是政策变化或重大事件引起的。如果是非系统风险，需要充分了解政策或重大事件后，决定是否调整策略，买入或出售相应资产以保障金融安全。判断系统风险的方法多种多样，较为流行的是通过历史价格信息预测未来价格，并比较真实价格与预测结果的差距。本项目将使用此方法进行股价预测，并与真实价格进行对比。

解决方案结构

为了实现对历史数据进行建模来预测未来价格，本篇采用如下结构的解决方案，同时大部分数据科学的项目也都可以使用类似的结构来完成：

1. 确定预测目标
2. 数据收集
3. 探索性数据分析
4. 数据预处理
5. 特征工程
6. 模型选择和训练
7. 模型评估
8. 模型预测

确定预测目标

在股票市场中，波动较大的股票并不少见。为了更好地了解市场状况，金融从业人员往往倾向于研究分析股票指数而非单个股票的价格。因为相对于单个股票来说，指数更稳定，更适合精准建模。指数通常由多种股票构成，广基指数（如道琼斯指数、标普500指数、日经指数、恒生指数等）一般反映市场绩效。这类指数不仅能反映股票市场的基本状况，还能体现投资者对经济现状的敏感度。

在本篇中，我选择的目标预测指数是标普500指数，这是全球最具标志性的追踪美国高市值公司的股票指数之一。

数据收集

收集金融数据的平台众多，其中像 Bloomberg、Qliq、Quandl 这样的国外市场平台，以及同花顺、万德这样的国内平台都受到大众的喜爱。大部分企业为了保证数据的准确性、安全性和时效性，在生产环境下会使用成熟的收费平台。在本篇中，我使用的是 Yahoo Finance，一个免费的公开金融数据平台，它不仅包含了大部分公开股票的实时数据，还提供了 Python API，可以通过股票代码和时间区间直接查询历史价格。

import yfinance as yf
df_sp = yf.download('^GSPC', start="2012-11-01", end="2022-11-01")

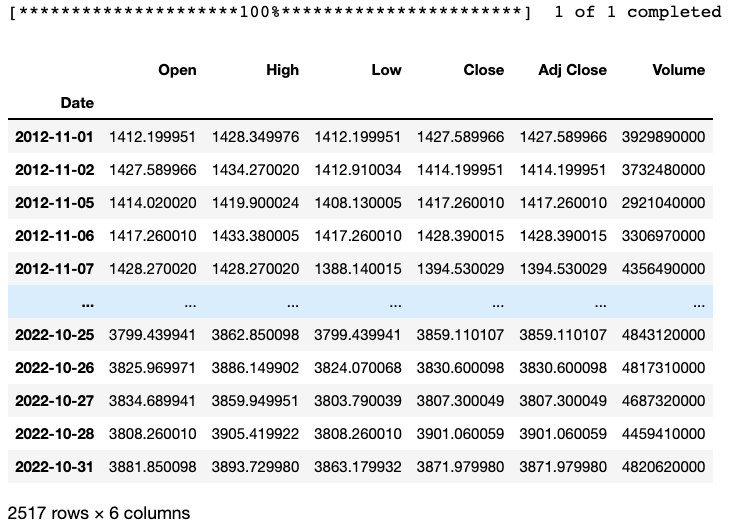
Pandas 数据集 df_sp 包含了从 2012 年 11 月 1 日至 2022 年 10 月 31日十年以来的标普 500指数数据，记录了每个日期所对应的开市价格、最高价格、最低价格、闭市价格、闭市调整价格和交易量。

探索性数据分析

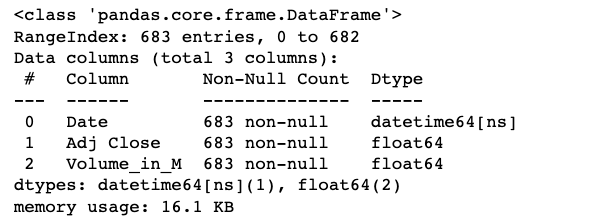
在收集完所需数据后，首先可以查看数据集中可能存在的空缺记录和需要调整的字段。我使用以下函数来了解数据集中包含多少条记录、是否有空缺值以及每个字段所对应的数据类型。

df_sp.info()

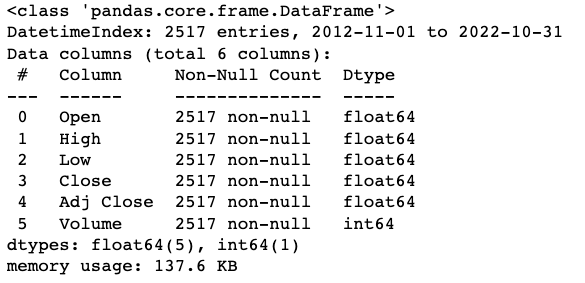
可以看到，数据集中没有需要处理的空缺值，并且每个字段的类型都是统一的。除日期以外（Python Datetime类型格式），其他字段都是数字类型。价格相关的都是浮点数，交易量相关的为整数。接下来，我通过以下函数查看数据的统计类信息。

df_sp.describe()

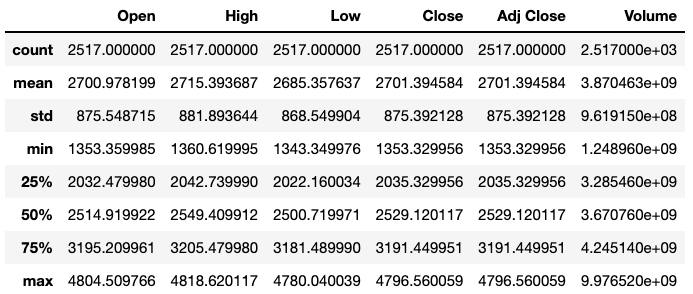
可以看到，指数数据都是正数，大部分以千为单位。唯一在单位上与其他列有所区别的是交易量数据。交易量的绝对数值与价格相比相差巨大。为了更有可比性，我需要调整交易量的绝对数值大小。在本步骤中，我选择先将交易量除以1000000，使其变成以百万为单位，那么在数值上，交易量数值大小缩小至千，与价格相似。

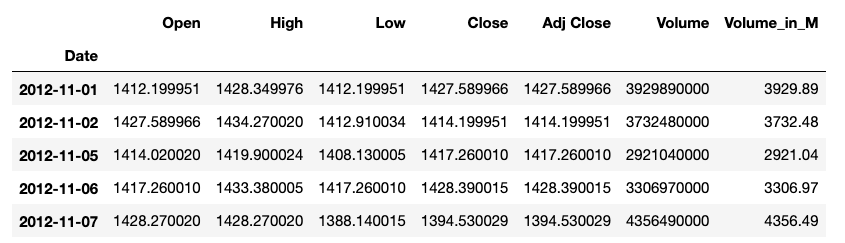
初步分析数据后，我可以将价格信息的时间序列可视化，更加直观地了解价格趋势。可使用相关性矩阵（correlation matrix）来研究变量之间的关系。

交易量与价格之间没有非常高的相关性，但这并不能证明交易量不应该在价格预测中被考虑。从另一个角度来说，各价格变量之间的相关性非常高，我只需挑选其中一个（闭市调整价格）进行预测即可。在下一步中，我只保留需要用到的信息即可。在本项目中，我的目标是使用自 2020 年 2 月 15日起的历史数据，预测未来 1个工作日的调整后闭市指数价格。为了发挥提取数据的最大价值，我需要对现有的两个变量进行一些处理，从而尽可能完整地展现数据的特性。特别是对于时间序列数据而言，季节性和周期性都是非常重要的信息，而这些信息是可以从时间序列本身提取的。必要的数据处理虽然会增加计算量，但可以换来更精准更完善的模型结果。

数据预处理

由于指数数据是时间序列，相比于大多数回归预测，我不仅要考虑模型需要什么样的变量，也需要考虑时间顺序。在本篇中，回归预测的数学公式如下，对于需要预测的未来在时间 时，价格可以表示为：

即利用 条历史记录来预测未来的价格。为提取有效信息以辅助预测，我将数据预处理大致分为以下四步：

1. 将时间转换为变量
2. 更改价格数据
3. 寻找周期和季节性
4. 根据周期调整交易量数据

将时间转换为变量

首先，我需要将时间信息从索引中提取出来。

df_mod_forecast = df_mod.reset_index()
df_mod_forecast.info()

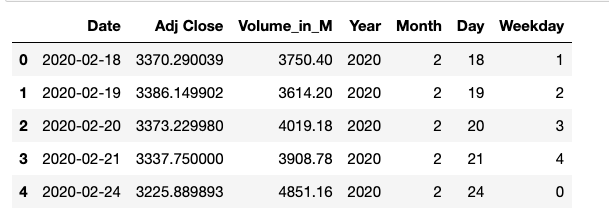
从日期信息中，提取年、月、日和工作日信息，经过处理后的数据如下：

df_mod_forecast.head()

更改价格数据

本篇的预测目标是未来价格，对于指数而言，金融从业者相对看重的是价格变动而非其数值的大小。我可以选择预测价格，也可以选择预测价格变动。我将根据数据本身的特性来决定二者当中谁更适合建模。

首先，我可以将每日和前一个工作日的价格差百分比计算出来。

df_mod_forecast['AdjPricePctDelta'] = df_mod_forecast['Adj Close'].pct_change()

寻找周期和季节性 — 解构时间序列与自相关分析

指数价格数据是以日期为单位的，且只有在工作日才有数据。我在尝试周期时可以有多种选择，例如以周、月或者季度为单位。这里时间序列分解效果最好的是月份。从2020 年 2 月到 2022 年 11 月大约有 20个月的时间。合适的周期会帮助我更好地寻找数据中的季节性。在之前的时间序列图像中注意到，全球疫情蔓延之后，股票市场表现出高于平常的波动。我需要使用multiplicative 模型来解决这个问题。我首先尝试分解价格的时间序列。

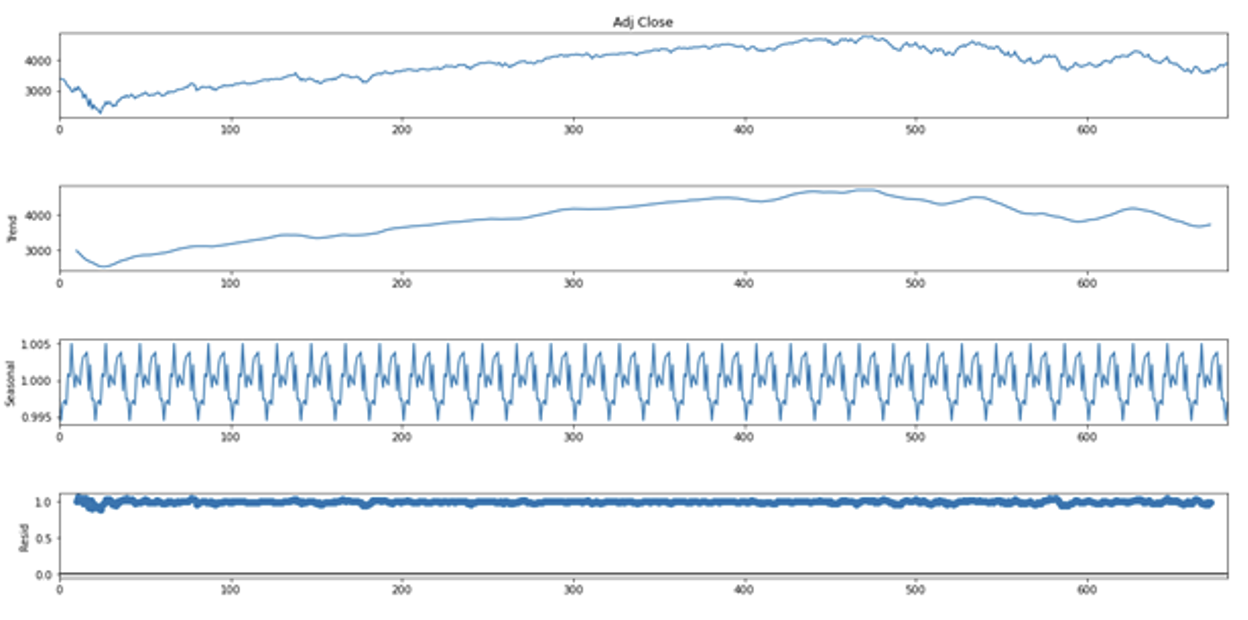
通过以上图像可以看出，每 100 天大约有 5 个周期，每个周期大约有 20天。除此之外，价格数据残差（residual）部分表现并不佳，徘徊在 1 左右。

根据周期调整交易量数据

时间序列较为传统的模型为 ARIMA模型，这类模型只需要一条时间序列，根据数据周期性等特征调试参数。时间序列也可以使用机器学习进行建模，这样的模型可以输入更多的变量，但需要对数据进行调整。和ARIMA 类型的模型不同，我需要使用 的价格波动和 的价格波动作为变量的一部分，输入模型进行训练。

在这里我需要运用 Pandas 的 shift方程，将价格变动数据分别下移一个和两个时间间隔。Shift方程需要索引作为时间的依据，因此我需要将日期设为索引。根据日期，将价格变动数据下移。

df_model['t_1_PricePctDelta'] = df_model['AdjPricePctDelta'].shift(periods=1)
df_model['t_2_PricePctDelta'] = df_model['AdjPricePctDelta'].shift(periods=2)

以此类推，我将交易量数据分别下移一个和两个时间间隔，两者求差即可得到每个交易日昨天（）与前天（）之间的交易量差。

df_model['t-1volume'] = df_model['Volume_in_M'].shift(periods=1)
df_model['t-2volume'] = df_model['Volume_in_M'].shift(periods=2)
df_model['t_1_VolumeDelta'] = df_model['t-1volume'] - df_model['t-2volume']

通过交易日前一天的价格变动，我可以将其转换为涨跌符号来作为模型输入的一部分。

df_model['sign_t_1'] = np.where(df_model['t_1_PricePctDelta'] > 0, 1, 0 * df_model['t_1_PricePctDelta'])

至此，完成了标普 500 指数数据从下载到转换的全过程。

特征工程

在正式建模之前，我需要对数据再进行特征工程，从而保证每个变量在模型训练中的公平性。根据现有数据的特点，我执行的特征工程流程大致有以下三个步骤：

1. 处理缺失值并提取所需变量
2. 数据标准化
3. 处理分类变量

处理缺失值并提取所需变量

首先，我需要剔除包含缺失值的行，并只保留需要的变量x_input，为下一步特征工程做准备。

x_input = (df_model.dropna()[['Year','Month','Day','Weekday','seasonality','sign_t_1','t_1_PricePctDelta','t_2_PricePctDelta','t_1_VolumeDelta']].reset_index(drop=True))
x_input.head(10)

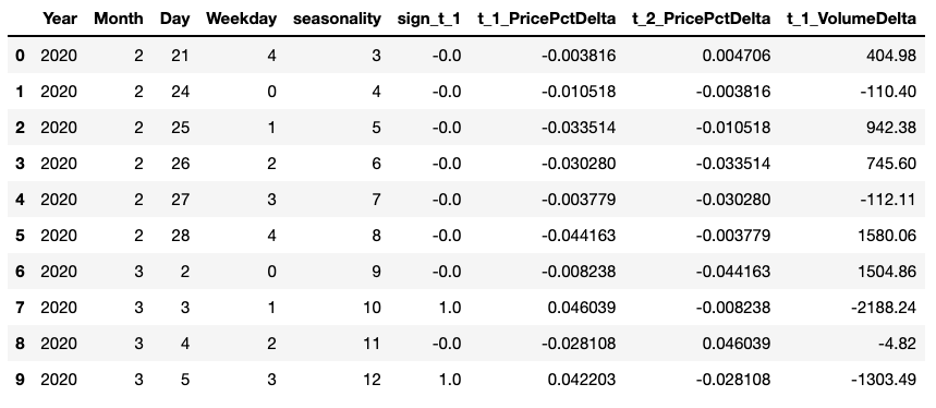
然后，再将目标预测列 y 从数据中提取出来。

y = df_model.dropna().reset_index(drop=True)['AdjPricePctDelta']

数据标准化

由于价格百分比差与交易量差在数值上有很大差距，如果不标准化数据，可能导致模型对某一个变量有倾向性。为了平衡各个变量对于模型的影响，我需要调整除分类变量以外的数据，使它们的数值大小相对近似。Python提供了多种数据标准化的工具，其中 sklearn 的 StandardScaler模块比较常用。数据标准化的方法有多种，我选择的是基于均值和标准差的标准化算法。这里，大家可以根据对数据特性的理解和模型类型的不同来决定使用哪种算法。比如对于树形模型来说，标准化不是必要步骤。

scaler = StandardScaler()
x = x_input.copy()
x[['t_1_PricePctDelta','t_2_PricePctDelta','t_1_VolumeDelta']] = scaler.fit_transform(x[['t_1_PricePctDelta','t_2_PricePctDelta','t_1_VolumeDelta']])

处理分类变量

最常见的分类变量处理方法之一是one-hot encoding。对于高基数的分类变量，经过编码处理后，变量数量增加，大家可以考虑通过降维或更高阶的算法来降低计算压力。

x_mod = pd.get_dummies(data=x, columns=['Year','Month','Day','Weekday','seasonality'])
x_mod.columns

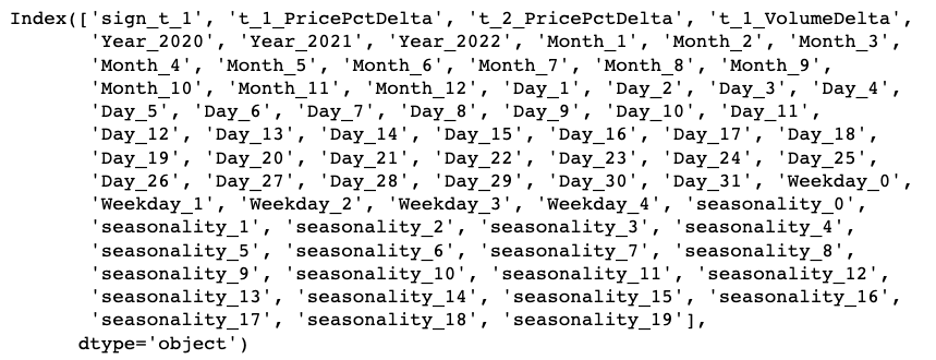
模型选择和训练

首先，我需要拆分训练集和测试集。对于不需要考虑记录顺序的数据，可以随机选取一部分数据作为训练集，剩下的部分作为测试集。而对于时间序列数据来说，记录之间的顺序是需要考虑的，比如我想要预测2 月份的价格变动，那么模型就不能接触 2月份以后的价格，以免数据泄露。由于股票指数数据为时间序列，我将时间序列前75% 的数据设为训练数据，后 25% 的数据设为测试数据。

模型选择

在模型选择阶段，我会根据数据的特点，初步确定模型方向，并选择合适的模型评估指标。

因为变量中包含历史价格和交易量，且这些变量的相关性过高（high correlation），以线性模型为基础的各类回归模型并不适合目标数据。因此，我模型尝试的重心将放在集成方法（ensemble method），以这类模型为主。

在训练过程中，我需要酌情考虑，选择合适的指标来评估模型表现。对于回归预测模型而言，比较流行的选择是MSE（Mean Squared Error）。而对于股票指数数据来说，由于其时间序列的特性，我在 RMSE的基础上又选择了 MAPE（Mean Absolute Percentage Error），一种相对度量，以百分比为单位。比起传统的MSE，它不受数据大小的影响，数值保持在 0-100 之间。因此，我将 MAPE作为主要的模型评估指标。

模型训练

在模型训练阶段，所有的候选模型将以默认参数进行训练，我根据 MAPE的值来判断最适合进一步细节训练的模型类型。我尝试了包括线性回归、随机森林等多种模型算法，并将经过训练集训练的各模型在测试集中的模型表现以字典的形式打印返回。

至此，完成了模型选择和训练的初步阶段，并评估了不同模型在测试集上的表现。

模型评估

通过运行以下方程，我可以根据预测差值（MAPE）的大小对各模型的表现进行排列。大家也可以探索更多种不同的模型，根据评估指标的高低择优选取模型做后续微调。

trail_result = ensemble_method_reg_trails(x_train, y_train, x_test, y_test)

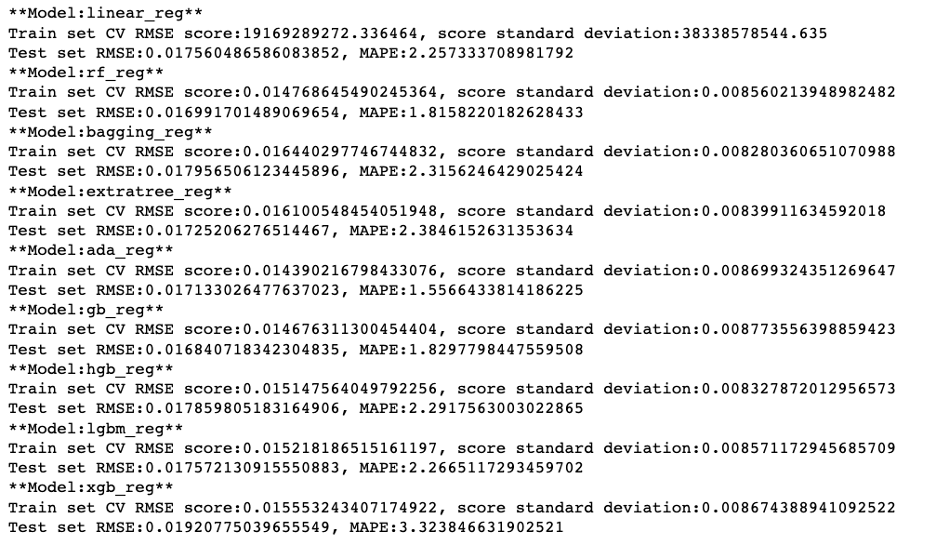
pd.DataFrame(trail_result).sort_values('model_test_mape', ascending=True)

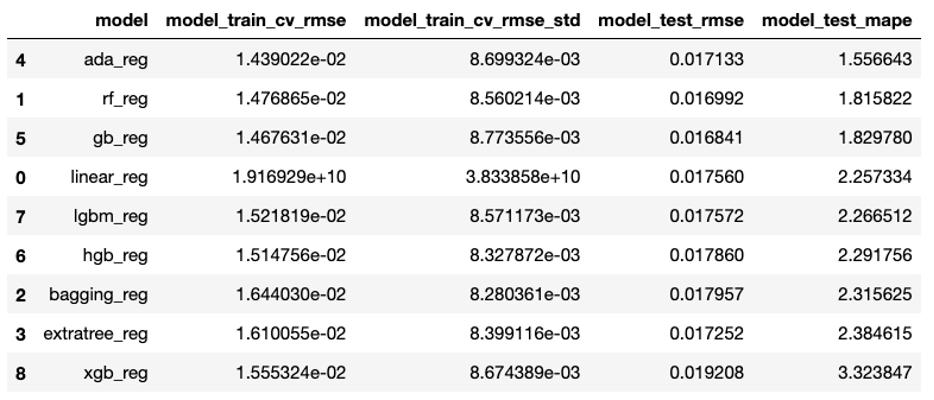
由此可以看出，在众多模型类型中，AdaBoost 在训练和测试集上的效果最好，MAPE 值最小，所以我选择 AdaBoost 进行下一步的细节调优。与此同时，我发现 Random Forest 和 GradientBoosting 也有不错的预测表现。注意，AdaBoost 虽然在训练集上准确度高，但模型的表现不是很稳定。

接下来的模型微调分为两个步骤：

1. 使用 RandomizedSearchCV 寻找最佳参数的大致范围
2. 使用 GridSearchCV 寻找更精确的参数

影响 AdaBoost 性能的参数大致如下：

• n_estimators
• base_estimator
• learning_rate

注意，RandomizedSearchCV 和 GridSearchCV都会使用交叉验证来评估各个模型的表现。在前文中我提到，时间序列是需要考虑顺序的。对于已经经过转换来适应机器学习模型的时间序列，每条记录都有其相对应的时间信息，训练集中也没有测试集的信息。训练集中记录的顺序可以按照特定的交叉验证顺序排列（较为复杂），也可以被打乱。这里，我认为训练集数据被打乱不影响模型训练。

base_estimator 是 AdaBoost 提升算法的基础，我需要提前建立一个base_estimator 的列表。

l_base_estimator = []
for i in range(1,16):
    base = DecisionTreeRegressor(max_depth=i, random_state=42)
    l_base_estimator.append(base)
l_base_estimator += [LinearSVR(random_state=42, epsilon=0.01, C=100)]

使用 RandomizedSearchCV 寻找最佳参数的大致范围

使用 RandomizedSearchCV，随机尝试参数。这里，我尝试了 500种不同的参数组合。

randomized_search_grid = {
    'n_estimators': [10, 50, 100, 500, 1000, 5000],
    'base_estimator': l_base_estimator,
    'learning_rate': np.linspace(0.01, 1)
}

search = RandomizedSearchCV(
    AdaBoostRegressor(random_state=42), 
    randomized_search_grid, 
    n_iter=500, 
    scoring='neg_mean_absolute_error', 
    n_jobs=-1, 
    cv=5, 
    random_state=42
)
result = search.fit(x_train, y_train)

可以看到，500 种参数组合中表现最佳的是：

result.best_params_

result.best_score_

使用 GridSearchCV 寻找更精确的参数

根据 RandomizedSearchCV 的结果，我再使用 GridSearchCV进行更深一步的微调：

• n_estimators: 1-50
• base_estimator: Decision Tree with max depth 9
• learning_rate: 0.7 左右

search_grid = {
    'n_estimators': range(1, 51),
    'learning_rate': np.linspace(0.6, 0.8, num=20)
}

GridSearchCV 的结果如下：

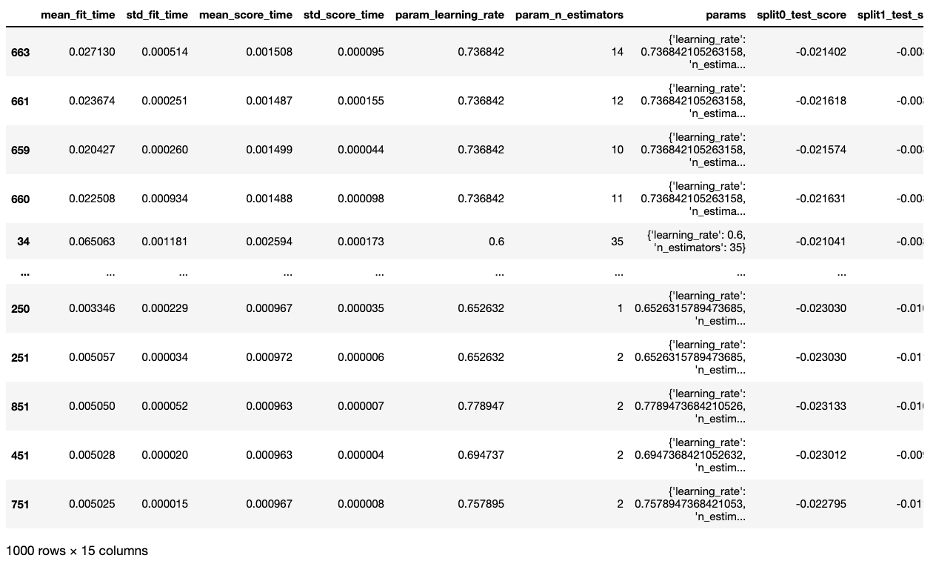
根据 GridSearchCV的结果，我保留最佳模型，让其在整个训练集上训练，并在测试集上进行预测，对结果进行评估。

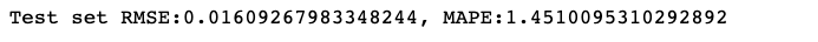
可以看到，结合训练集的交叉验证结果，最佳模型在测试集中的表现与模型选择和训练阶段的结果相比，准确度略有提升。最佳模型平衡了训练集和测试集表现，可以更有效地防止过拟合的情况出现。该模型在全量数据的预测结果中 MAPE 值为：

模型预测

与传统的 ARIMA模型不同，现有模型的每次预测都需要将预测信息重新整合，输入进模型后才能得到新的预测结果。输入数据的重新整合可以用以下方程进行开发，方便适应各种应用场景的需求。

def forecast_one_period(price_info_adj_data, ml_model, data_processor):
    last_record = price_info_adj_data.reset_index().iloc[-1,:]
    next_day = last_record['Date'] + relativedelta(days=1)
    next_day_t_1_PricePctDelta = last_record['AdjPricePctDelta']
    next_day_t_2_PricePctDelta = last_record['t_1_PricePctDelta']
    next_day_t_1_VolumeDelta = last_record['Volume_in_M'] - last_record['t_1_VolumeDelta']
    if next_day_t_1_PricePctDelta > 0:
        next_day_sign_t_1 = 1
    else:
        next_day_sign_t_1 = 0
    next_day_input = (pd.DataFrame({'Date':[next_day],
                                    'Volume_in_M':[-99999],
                                    'AdjPricePctDelta':[-99999],
                                    't_1_PricePctDelta':[next_day_t_1_PricePctDelta],
                                    't_2_PricePctDelta':[next_day_t_2_PricePctDelta],
                                    't-1volume': last_record['Volume_in_M'],
                                    't-2volume': last_record['t-1volume'],
                                    't_1_VolumeDelta':[next_day_t_1_VolumeDelta],
                                    'sign_t_1':next_day_sign_t_1}).set_index('Date'))
    if next_day > datetime.datetime(2020, 2, 15):
        price_info_adj_data = price_info_adj_data[price_info_adj_data.index > datetime.datetime(2020, 2, 15)]
    price_info_adj_data_next_day = pd.concat([price_info_adj_data, next_day_input])
    input_modified = data_processor.data_modification(price_info_adj_data_next_day)
    x,y = data_processor.data_modeling_prep(input_modified)
    next_day_x = x.iloc[-1:]
    forecast_price_delta = ml_model.predict(next_day_x)
    forecast_df = {'Date':[next_day], 'price_pct_delta':[forecast_price_delta[0]], 'actual_pct_delta':[np.nan]}
    return pd.DataFrame(forecast_df)

我读取之前保存的模型，对未来一个工作日的价格变动进行预测。输出的结果actual_pct_delta 是为未来价格发布后保存真实结果所预留的结构。

import pickle
with open('best_model.pkl', 'rb') as file:
    best_reg = pickle.load(file)
forecast_df = forecast_one_period(price_info_adj_data, best_reg, data_processor)
print(forecast_df)

根据预测结果，我认为 2022 年 11 月 1 日这天标普指数会有轻微的上升。

分析预测结果

根据近两年的数据走向，我有了这样的预测结果：标普指数会有轻微的上升。但当我查看2022 年 11 月 1日发布的实际数据时发现，指数在当天是下降的。这意味着外界的某种信息，可能是经济指标抑或是政策风向的改变，导致市场情绪有所变化。搜索相关新闻后，我发现了以下信息：

在经济面临多重考验的同时，招聘市场职位数量上升的信息释出，导致投资者认为招聘市场表现稳健，美联储不会考虑放宽当下的经济政策；这种负面的展望在股票市场上得到了呈现，导致当日指数收盘价下降。

模型在实际应用中不仅仅充当着预测的工作，在本项目的案例中，指数价格变动的预测更类似于一种 “标线”。通过模型学习历史数据，模型的结果代表着如果按照历史记录的信息，没有外部重大干扰的情况下，我所期待的变动大致是怎样的，即当日实际发生的变动是“系统”层面的变动，还是需要深度挖掘的非“系统”因素所造成的变动。在模型的基础上，在以后的学习生活中，我可以将这些结果举一反三，开发出各式各样的功能，让数据尽可能地发挥其价值。